Класификационни и регресионни дървета¶
In [1]:
from sklearn.datasets import make_classification
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
%matplotlib inline
Днес: decision trees
Преди това: да си припомним малко от предния път.
NumPy и векторизация¶
Повечето операции в NumPy работят с така наречената векторизация. Това по-лесно се илюстрира с пример:
In [2]:
np.array([1, 2, 3, 4]) * 5
Out[2]:
In [3]:
np.array([1, 2, 3]) * np.array([3, 4, 5])
Out[3]:
In [4]:
np.array([8, 3, 4, 1, 9, 4]) > 4
Out[4]:
In [5]:
(np.array([8, 3, 4, 1, 9, 4]) > 4).astype(float)
Out[5]:
In [6]:
np.array([10, 20, 30])[np.array([1, 0, 2, 0, 1])]
Out[6]:
LabelEncoder¶
Ако има категорийни данни (например низове), може да ползваме LabelEncoder да ги заменим с числа:
In [7]:
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
encoder.fit(["red", "green", "red", "blue", "red", "green"])
colors = ["green", "green", "blue"]
print("transofrmed:", encoder.transform(["green", "green", "blue"]))
print("inverse: ", encoder.inverse_transform([0, 1, 2]))
OneHotEncoder¶
Може да кодираме категории с label encoder, когато в категориите има някакъв естествен ред (напр. 4 е по-голямо от 2). Ако няма такъв ред обаче, на най-добре е да ползваме one-hot – така създаваме по един фийчър за всяка категория, който има стойности 0 или 1.
In [8]:
from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder()
encoder.fit([[0],
[1],
[0],
[2]])
print(encoder.transform([[0], [1], [1], [2], [0]]).toarray())
Но да се върнем към днешната тема!
In [9]:
x, y = make_classification(n_samples=100,
n_features=2,
n_redundant=0,
n_clusters_per_class=2,
random_state=123)
In [10]:
print(x[:4])
print(y[:4])
In [11]:
plt.scatter(x[:,0], x[:,1], c=y);
In [12]:
# Plotting decision regions adapted from
# http://scikit-learn.org/stable/auto_examples/ensemble/plot_voting_decision_regions.html
def plot_boundary(clf, X, y):
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
np.arange(y_min, y_max, 0.1))
f, ax = plt.subplots(figsize=(10, 8))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
ax.contourf(xx, yy, Z, alpha=0.4)
ax.scatter(X[:, 0], X[:, 1], c=y, s=20, edgecolor='k')
plt.show()
In [13]:
clf = DecisionTreeClassifier().fit(x,y)
print(clf.score(x, y))
scores = cross_val_score(clf, x, y, cv=5)
print(scores)
print(scores.mean())
Как се учи алгоритъмът?¶
In [14]:
clf = DecisionTreeClassifier().fit(x, y)
plot_boundary(clf, x, y)
In [15]:
clf = DecisionTreeClassifier(min_samples_split=50).fit(x, y)
plot_boundary(clf, x, y)
In [16]:
import graphviz
dot_data = tree.export_graphviz(clf, out_file=None)
graph = graphviz.Source(dot_data)
graph.render("tree")
dot_data = tree.export_graphviz(clf, out_file=None,
feature_names=np.array(['X_0 Vertical', 'X_1 Horizontal']),
class_names=np.array(['Class_0', 'Class_1']),
filled=True, rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data)
In [17]:
graph
Out[17]:
Моделът CART е двоично дърво.¶
- Всеки елемент от дървото може да има нула, едно или две деца.
Алгоритъмът работи рекурсивно.¶
Критерии за спиране могат да бъдат:¶
- Достигната е абсолютна чистота на елементите в дървото. (останали са само един клас данни в последните деца)
- Достигната е максимална дълбочина на дървото. (max_depth)
- Достигнат е минимален брой примери за разделяне. (min_samples_split)
Алгоритъмът е алчен (greedy):¶
- Проверява всяка възможна колона (feature) за всички възможни раздвоявания и избира най-доброто.
- Сложност при трениране: $O(n_{features}n_{samples}\log(n_{samples}))$
Оценяваща функция:¶
- Оценяващата функция работи, чрез Information Gain: $$ InformationGain = impurity(parent) - {WeightedAverageBySamplesCount}\sum{impurity(children)}$$
Измерване на "примеси"(Impurity measures)¶
Класификация:¶
- Ентропия (Entropy)
- Gini
- Неправилна класификация (Misclassification)
Регресия:¶
- Средно аритметично от разликата на квадратите (Mean Squared Error)
- Средно аритметично от абсолютната стойност на разликата (Mean Absolute Error)
При предвиждане на нов запис, алгоритъмът се спуска по построеното дърво докато стигне възел без наследници.¶
- Предвижда средната стойнoст от записите останали в последния елемент при регресия.
- При класификация избира класа представен от мнозинството от записи останали в последния елемент.
- Сложност при предвиждане: $O(\log(n_{samples}))$
Измерване на примесите (impurity)¶
Пример:¶
['Лъчо', 'Лъчо', 'Стефан', Стефан']
Лъчо - 2, Стефан - 2
Пропорции:
Лъчо: $\frac{2}{4}$, Стефан: $\frac{2}{4}$
Стойност за Лъчо: $$-\frac{2}{4} * log_2(\frac{2}{4})$$ $$-0.5 * -1$$ $$0.5$$
Стефан има същата стойност $0.5$.
Ентропията на множеството е $$entropy=0.5+0.5 = 1.0$$
Пример 2:¶
['Круши', 'Круши', 'Круши']
Круши - 3
Пропорции:
Круши $\frac{3}{3} = 1$
$$-1 * log_2(1)$$ $$-1 * 0$$ $$entropy=0$$
In [18]:
def entropy(subset_counts):
subset_counts = np.array(subset_counts)
subset_counts_normalized = subset_counts / subset_counts.sum()
entropy = sum([-subset_count * np.log2(subset_count +0.000000000001)
for subset_count in subset_counts_normalized])
entropy = np.round(entropy, 4)
print('Entropy for', subset_counts, " is:", entropy)
return entropy
In [19]:
samples = [[2,0], [1,0], [9,1], [4,4]]
for sample in samples:
entropy(sample)
In [20]:
samples = [[2,0,1], [6,0,0], [9,1,0], [5,5,0], [5,5,5]]
for sample in samples:
entropy(sample)
Gini¶
$H(X_m) = \sum_k p_{mk} (1 - p_{mk})$
Пример:¶
['Лъчо', 'Лъчо', 'Стефан', Стефан']
Лъчо - 2, Стефан - 2
Пропорции:
Лъчо: $\frac{2}{4}$, Стефан: $\frac{2}{4}$
Стойност за Лъчо: $$-\frac{2}{4} * (1 - \frac{2}{4})$$ $$-0.5 * -0.5$$ $$0.25$$
Стефан има същата стойност $0.25$.
$$gini=0.25+0.25 = 0.5$$
Пример 2:¶
['Круши', 'Круши', 'Круши']
Круши - 3
Пропорции:
Круши $\frac{3}{3} = 1$
$$1 * (1 - 1)$$ $$1 * 0$$ $$gini=0$$
In [21]:
def gini_impurity(subset_counts):
subset_counts = np.array(subset_counts)
subset_counts_normalized = subset_counts / subset_counts.sum()
impurity = sum([subset_count * (1 - subset_count)
for subset_count in subset_counts_normalized])
print('Gini impurity for', subset_counts, " is:", impurity)
return impurity
In [22]:
samples = [[2,0], [1,0], [9,1], [4,4]]
for sample in samples:
gini_impurity(sample)
In [23]:
samples = [[2,0,1], [6,0,0], [9,1,0], [5,5,0], [5,5,5]]
for sample in samples:
gini_impurity(sample)
Неправилна класификация (Misclassification)¶
$H(X_m) = 1 - \max(p_{mk})$
In [24]:
def missclassification_impurity(subset_counts):
subset_counts = np.array(subset_counts)
subset_counts_normalized = subset_counts / subset_counts.sum()
impurity = 1 - max(subset_counts_normalized)
print('Misclassification impurity for', subset_counts, " is:", impurity)
return impurity
In [25]:
samples = [[2,0], [1,0], [9,1], [4,4]]
for sample in samples:
missclassification_impurity(sample)
In [26]:
samples = [[2,0,1], [6,0,0], [9,1,0], [5,5,0], [5,5,5]]
for sample in samples:
missclassification_impurity(sample)
Information Gain¶
$ InformationGain = impurity(parent) - {WeightedAverageBySamplesCount}\sum{impurity(children)}$
In [27]:
def information_gain(subsets, parent_entropy=1, f=entropy):
total_count = sum([sum(i) for i in subsets])
print("total count:", total_count)
subsets_impurity = sum((sum(subset) / total_count * f(subset) for subset in subsets))
IG = parent_entropy - subsets_impurity
print("Information gain:", IG)
return IG
In [28]:
subsets = [[2,1], [1]]
for f in [entropy, gini_impurity, missclassification_impurity]:
information_gain(subsets, parent_entropy=1, f=f);
print();
In [29]:
subsets = [[2], [2]]
for f in [entropy, gini_impurity, missclassification_impurity]:
information_gain(subsets, parent_entropy=1, f=f);
print();
In [30]:
graph
Out[30]:
In [31]:
gini_impurity([48,52])
gini_impurity([9, 49])
gini_impurity([39, 3])
gini_impurity([0, 46]);
Плюсове:¶
- Дървото е лесно за интерпретация.
- Лесно се справя с ирелевантни атрибути - фичъри (gain =0).
- Може да се справи с липсващи данни. (Не и за текущата имплементация в sklearn).
- Компактно представяне на модела.
- Бърз при предсказване O(дълбочината на дървото).
- Може да прави класификация с повече класове без допълнителни трикове.
- Лесен за използване и дава добри резултати с малко експерименти.
Минуси:¶
- Разделя атрибутите само по осите.
- Алчен (greedy) - може да не открие най-доброто дърво.
- Експоненциално нарастване на възможните дървета.
- Овърфитва силно.
Въпроси по DT?¶
Random Forest¶
In [32]:
from sklearn.ensemble import RandomForestClassifier
In [33]:
clf = RandomForestClassifier(random_state=23).fit(x,y) # без натройка на параметрите
plot_boundary(clf, x, y)
Параметри за RF:¶
- n_estimators: брой дървета - 10, 100, 1000
- criterion: за всички дървета - gini, entropy
- max_features: Колко фичъра да се пробват при търсене на най-добро разделяне. sqrt(n_features) - различни при всяко ново търсене.
- max_depth: Максимална дълбочина на дърветата
- min_samples_split: Минимален брой семпли за да може да се раздели възела
- bootstrap - Втори параметър за случайност - random sampling with replacement. Тегли същия брой семпли като оригиналния сет.
- n_jobs - Тренира по няколко дървета едновременно, но използва повече памет.
- random_state - възпроизведими експерименти
In [34]:
clf = RandomForestClassifier().fit(x,y)
plot_boundary(clf, x, y)
In [35]:
clf = RandomForestClassifier().fit(x,y)
plot_boundary(clf, x, y)
Значимост на фичърите в RF - Сходно на теглата на параметрите при линейни модели.¶
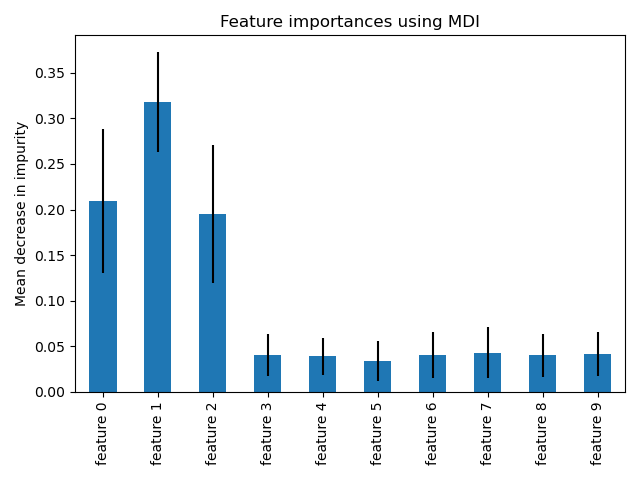http://scikit-learn.org/stable/auto_examples/ensemble/plot_forest_importances.html